A scope-based technique for optimizing EMI input filters

A simple oscilloscope setup can size common-mode and differential-mode noise filtering components separately and more accurately.
Marcus Sonst, Rohde & Schwarz

Any switched-mode power supply (SMPS) needs an EMI (electromagnetic interference) input filter to avoid disturbing power lines. Input filters generally contain both common-mode and differential-mode filter elements, and the two are rarely optimized separately. In particular for high-power applications, this practice can result in a significantly larger EMI filter than actually necessary.

But a simple procedure using a dual-output LISN (Line Impedance Stabilization Network) and an oscilloscope can optimize common-mode and differential-mode noise components separately. The result is more accurate data for designing an optimal input filter.

An SMPS generates a fair amount of noise. The choice of SMPS topology is significant and influences filter design. For example, a dual-interleaved boost topology creates less noise than a simple boost converter. For a given topology, there are several design parameters that influence noise levels. The switching frequency of the converter is key. Often, a high switching frequency is chosen in the interest of a compact design but at the cost of more EMI.

It is important to understand the correlation between rise and fall time of the switching element and the generated noise. Nowadays, wide-bandgap devices based on SiC or GaN are more widely used in power converter designs to boost efficiency. These technologies are known for their fast switching and potential for generating EMI in the absence of mitigation measures. Parasitic elements can also play a role. For example, a metal housing near a high-voltage switching element can create a parasitic capacitance acting as a path for common mode noise to leave the system.

The key components for the differential-mode EMI filter in an ac/dc converter are the differential-mode inductors and the X-capacitors. For the common-mode EMI filter, the common-mode choke and the Y-capacitor are key. In some cases, the differential-mode inductors can be omitted as the common-mode choke can also act as differential mode inductor.

Electromagnetic compatibility standards require measurement of the conducted emissions on both power lines and dictate that the EMI voltages remain below specified limits at all frequencies in the range. This measurement takes place first on one power line, then the other. Unfortunately, this procedure provides no insights into noise propagation mechanisms because it measures common-mode and differential-mode noise simultaneously.

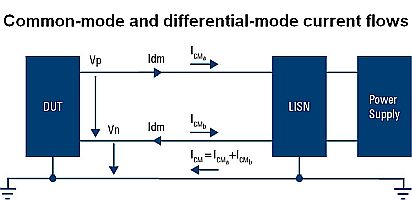
The common mode current I_cm flows from the DUT (device under test) on both power lines into the LISN and to the DUT back via the external ground path. Thus the sum of the two currents flow to the external ground path. The amplitude and phase are the same on both conductors. The differential mode current has a different characteristic; the current on the positive conductor flows into the LISN while the noise return path is the negative conductor. The only difference is the phase between these two currents; they differ by 180° and ideally should cancel out.

A little mathematics separates the common-mode (CM) and differential-mode (DM) noise terms. Using the individual currents:

I_P = I_CMa + I_DM

I_N = I_CMb – I_DM

we can easily calculate the voltages on the two conductors:

V_P = (I_CMa + I_DM) × Z_LISN

V_N = ( I_CMb − I_DM) × Z_LISN

Based on the relations between individual voltages and common-mode and differential-mode voltages:

V_P + V_N = V_CMa + V_CMb

we can calculate the common-mode and differential-mode voltages as follows:

V_CM = V_P + V_N

V_DM = ½ (V_P − V_N)

The simple subtraction results in a value that is twice the differential mode noise level, or 6 dB extra. Using these simple calculations, we distinguish between common-mode noise and differential-mode noise (including subtraction of 6 dB from the differential result). The simple calculation works well if the setup (cable, components of the LISN, etc.) is as symmetrical as possible; the noise on the two conductors must be measured simultaneously.

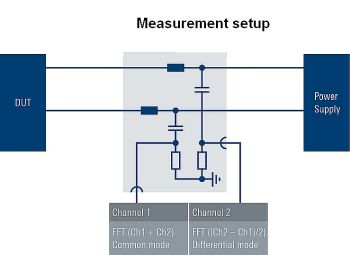
A simple but effective setup to separate common-mode and differential-mode noise employs a dual-output LISN (or two identical LISNs) to probe both power lines. The two signals are captured on two channels of an oscilloscope. The sum and difference signals are calculated on the scope as is the (Fast Fourier Transformation) FFT. The result is direct access to the common-mode and differential-mode noise.

While any non-symmetry between the two LISNs will influence the measurement result, this method provides reasonably accurate results. It is important that the setup use cables of identical length and cables with sufficient quality to avoid a shift in time or loss in amplitude. Such factors degrade the ability to separate the noise components. Furthermore, the oscilloscope needs a sufficiently low-noise front end and a sufficiently fast FFT function.

To help illustrate this method, consider the case of a simple step-down buck converter DUT. Its input filter is a simple PI-LC configuration which is effective for damping differential-mode noise. The setup simplifies the task of either applying or excluding the PI-LC filter. No common-mode filters are included on the PCB, so a common-mode choke is attached externally. The converter has no housing; the PCB simply sits on an isolation block that is on a metal ground plane. The setup deliberately avoids generating excessive common- mode noise.

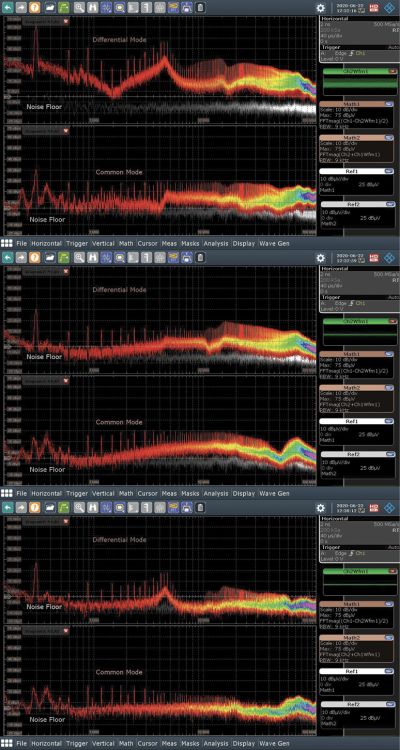
The first measurement is taken to show the highest spectrum in the input power conductors. A reference level measurement establishes the noise level of the system while the DUT is switched off. The extra 6 dB in differential mode is compensated by dividing the sum expression by two, then performing the FFT. For common mode, the sum expression is used directly. The total amount of common-mode noise is represented by the sum of the two measurement channels.

The peak at 300 kHz in the reference line is caused by the system, not the converter, and can be ignored at least up to 25 dBµV. The high differential-mode noise (approximately 65 dBµV) during the measurement at 300 kHz arises from the switching frequency of the converter. The harmonic and all higher odd multiples of this frequency stem from the reflected ripple current, which dominates the differential-mode spectrum.

Some peaks are also visible in the common mode spectrum; these are not filtered by a differential filter.

Calculations show an LC filter will damp the fundamental at 300 kHz. The calculated filter resonance frequency is at 19.3 kHz, which should suppress the switching frequency by 40 dB. The filter structure is of second order and thus the damping is about 40 dB/decade.

The differential-mode noise is efficiently reduced up to 10 MHz, damped up to 30 dB compared to the unfiltered value. The magnitude of the fundamental at 300 kHz and the multiple harmonics are much lower. At higher frequencies the filter is less effective, damping noise only by 10 dB.

The filter doesn’t affect common-mode noise significantly because the it was designed to filter differential- mode noise. Another filter is added to damp common mode noise, taking the form of a common-mode choke from Würth Electronic.

The common-mode noise is greatly reduced from 2 MHz to 60 MHz. In addition, the differential-mode noise is also damped as the common-mode choke is not ideal. The resulting leakage inductance functions as a differential filter. Furthermore, the differential-mode noise may also be affected if the setup is not optimized (no PCB for the common-mode choke). Thus some asymmetrical components may cause this additional damping effect.

All in all, an effective input filter helps fulfill EMI standards for SMPS conducted emissions. Accurate information about the common-mode and differential-mode noise contributions greatly aids the task of designing and optimizing the EMI input filter.