The digital oscilloscope currently dominates the market, both in bench-type and hand-held instruments produced by all major manufacturers. But back in the day, cathode ray tubes were used to display analog signals, which were processed by linear amplifiers. The advantage of digital technology for the oscilloscope is much faster processing and the ability to store waveforms for all kinds of analysis including Fourier translation from time domain to frequency domain.
Because the inputs are usually analog, digitization is required close to the front end of the instrument. The method by which this takes place is known as sampling. The advantage of this configuration over the all-analog oscilloscope is that the signal(s) can be stored in digital memory without degradation. This permits complex processing of the signal by high-speed digital processing circuits. For this to work, there must be a sufficient number of samples per unit of time. If too few samples are deployed, an accurate digital representation will not be possible.
The minimum number of samples per unit of time required to unambiguously capture an analog signal is quantified by the Nyquist theorem. This theorem is strictly applicable for mathematical functions whose Fourier transform is zero outside of a limited band of frequencies. That is simply another way of saying that the signal must have a finite bandwidth, which is ordinarily the case anyway.
It is clear that if a continuous function (analog signal) is reduced to a discrete series and subsequently interpolated back to a continuous function (as within a digital scope between the analog input and the final display), the signal fidelity will depend on the sampling density. The Nyquist theorem gives the sampling rate necessary to attain signal fidelity. The minimum required sampling rate is a function of the bandwidth of the original signal, which is why that bandwidth must be finite.
The Nyquist theorem states that for perfect signal reconstruction, the sampling rate must be twice the bandwidth, which is to say B ≤ fs/2. A lesser sampling rate will sometimes yield acceptable fidelity, especially when there are additional constraints on the bandwidth, but in these instances, while acceptable fidelity may be achieved, it cannot be assured.
Furthermore, because the bandwidth of signals we encounter is typically gaussian rather than having sharp high and low cutoffs, still faster sampling rates are appropriate and typically supplied by oscilloscope manufacturers.
The most common type of sampling, what we might call “regular” sampling, is known as real-time sampling. Real-time sampling is used in a real-time sampling oscilloscope Equivalent-time sampling is used in an equivalent-time sampling oscilloscope. These are usually two different types of instruments, although there are exceptions. For example, B&K Precision Corp.’s BK 2510 Series oscilloscopes incorporate both types of sampling. To switch between the two modes, press scope, then acquire. F4 toggles between real-time and equivalent-time sampling modes. For most work, you’ll stay with the real time sampling.
A real-time oscilloscope captures the entire waveform between two successive trigger events. Thus, even if the waveform is non-repetitive, the acquisition will be complete. (A repeating waveform is not required in real-time sampling.) Samples are taken in response to a high-speed clock. Every time there is a pulse, a sample is taken. These samples are taken at the sampling rate, which is constant for any given oscilloscope, always greater than twice the bandwidth of the oscilloscope.
The clock pulses are not synchronized to nor dependent upon the frequency of the signal at the input. In instruments of high bandwidth, this method places great demands on the oscilloscope manufacturer and on the user in terms of cost. For this reason, the expedient of equivalent sampling was developed.

In equivalent sampling, the waveform amplitude is also measured at the sampling instant, but this happens only one time in each cycle. In the next cycle, a tiny delay is added, after which another sample is taken. Continuing in this mode, the waveform can be reproduced after a sufficient number of cycles have elapsed, so the full number of samples are accumulated. This makes a high sample count possible, but the pace is more leisurely. It also makes high instrument bandwidths viable.
There are some requirements for equivalent-time sampling to work. The signal must be repetitive. A single-shot signal can be rendered digitally only by using real-time sampling. In the equivalent-time sampling mode, moreover, there must be an explicit trigger event, and it must be synchronous with the input data on an ongoing basis. The trigger can be user-supplied or derived from clock circuitry.
In equivalent-time sampling, the first sample is initiated by the trigger event. The next trigger begins the sampling action, which actually takes place after a precise delay. Subsequent samples are accumulated, and the entire waveform is acquired, whereupon the process repeats so the oscilloscope can operate in the run mode.
In an equivalent-time sampling oscilloscope, data may be viewed as a bit stream or as an eye diagram. In the bit-stream mode, the trigger event happens once during the cycle, and it must be in the same relative position in the bit pattern.
In contrast, to create an eye diagram in the equivalent-time sampling mode, a repetitive waveform is not necessary. Noise, jitter, distortion and signal strength are revealed among other properties. But a synchronous clock signal is mandatory.
Recent real-time sampling oscilloscopes are also able to display signals in the eye diagram format. To create an eye pattern, an oscilloscope continuously samples the signal-of-interest and applies it to the vertical input. Simultaneously, the data rate triggers the horizontal sweep.
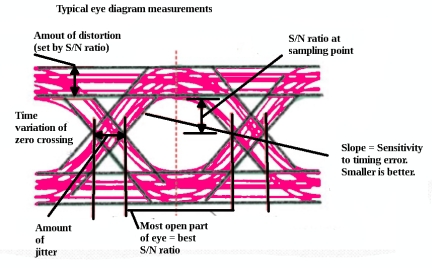 Because special use is made of the analog inputs, eye patterns are akin to Lissajous patterns. In both instances, what you see on the screen does not look at all like a conventional time-domain representation of an electrical signal. (The eye pattern gets its name from the fact that it resembles a pair of eyes peering out between two horizontal lines.) Power is represented on a vertical scale and time on a horizontal scale. We see channel noise and intersymbol interference as they effect the system of interest.
Because special use is made of the analog inputs, eye patterns are akin to Lissajous patterns. In both instances, what you see on the screen does not look at all like a conventional time-domain representation of an electrical signal. (The eye pattern gets its name from the fact that it resembles a pair of eyes peering out between two horizontal lines.) Power is represented on a vertical scale and time on a horizontal scale. We see channel noise and intersymbol interference as they effect the system of interest.
Real-time and equivalent-time oscilloscopes each have advantages. For a real-time sampling instrument, an explicit triggering event is not always needed. It can display single-shot transient events without benefit of a repetitive waveform. Cycle-to-cycle jitter can be directly measured. Troubleshooting is easier because the latest real-time sampling oscilloscopes incorporate large record lengths and deep memories.
Equivalent-time sampling oscilloscopes having high bandwidths are less costly due to reduced sampling demands. The lower sampling rate provides higher resolution at the point of analog-to-digital conversion and also gives wider bandwidth, lower noise floor, and less intrinsic jitter.
As noted above, signal transformation of waveform information in an oscilloscope is a two-stage process. First, the analog signal is sampled at a Nyquist-compliant rate so as to create a digital version. Then, the signal must be rendered without loss or distortion as an analog representation if it is to be displayed in conventional time-domain form on the oscilloscope screen.
Signal reconstruction (from digital to analog) can take place in a number of ways. The most common method in today’s amazing oscilloscopes is by means of Sin(x)/x interpolation.
To prevent aliasing, an anti-alias filter is sometimes used to reject high-frequency content of the signal that is in excess of that permitted by the Nyquist theorem. Another approach is to boost the sample rate, which is sometimes less costly. The choice between a real-time and equivalent-time sampling involves several decisions in terms of anticipated usage (single-shot or repetitive waveforms). Cost plays a significant but not always defining role.

Leave a Reply
You must be logged in to post a comment.