Amateur astronomers like to build their own telescopes, sometimes to the point of even grinding the objective mirrors. This is doable, but involves purchasing the mirror blank plus various grades of grinding abrasives, polishing compounds and specialized tools.

The lens must have a precise parabolic profile. It takes special test instruments to figure out whether the lens profile is really parabolic. In early stages, necessary tools include a laboratory-grade straight-edge and eventually a Foucault tester. The Foucault test was devised in the 19th century to accurately ascertain the status of concave mirrors in the final stages of grinding and polishing. It measures surface dimensions by reflecting light past a knife edge at or near the mirror’s center of curvature.

A high-quality Foucault tester with a built-in knife edge and light source can be purchased on-line for under $200, or it can be easily fabricated. It consists of a light source, razor blade and metal foil with a pinhole opening. The device is adjustable relative to the knife edge and the optical axis, and it can be moved in 0.001-in increments to detect errors in the mirror’s curvature to a millionth of an inch!

To use the Foucault tester, the user places the tester at twice the focal length of the mirror under investigation. Viewing the mirror from behind the knife edge reveals errors in the mirror’s parabolic curvature, which can be progressively polished out. Any high spots or depressions are greatly magnified.

To understand Foucault testing, consider the simple case of Foucault testing a spherical mirror. The light source would be near the knife edge. The knife edge cuts reflected rays from the mirror, and an observer would see a shadowgram, as close as possible to the knife edge. The light source and knife edge sit at the radius of curvature (RoC) for the mirror. Light strikes every location of the mirror exactly perpendicular to the surface, and is reflected exactly back on itself. Thus the rays will reflect to a point focus exactly at the RoC. When the knife edge cuts into this reflected beam at the radius of curvature, it cuts off all the light because at focus the returned light cone is a single small point. So the observer sees a sharp, quick darkening of the mirror with no observed shadows or shadow motion.

If the knife edge sits closer to the mirror then the focus at radius of curvature, the knife won’t cut all the reflected rays simultaneously. Instead it cuts off the rays from one side of the mirror first, then the center, and finally the rays reflected from the other side. The result is a dark shadow moving across the mirror, traveling in the same direction the knife edge. As the knife edge approaches the radius of curvature, the shadows move faster as it cuts more rays because they are spaced closer together.

When the knife edge is outside of the radius of curvature, the direction of the shadow travel reverses. Thus if the shadows move in the same direction as the knife edge, the knife sits inside the RoC. If the shadows move in the opposite direction as the knife edge, the knife sits outside the RoC. If there’s no shadow motion but the zone ‘blinks’ dark, the knife is at the RoC.

On a complex optical surface, or where the lens hasn’t been ground to a perfect radius, each part of the surface will likely have a different RoC. So the reflected rays will focus at different points. In these cases the resulting shadowgrams can get quite complex. In doing testing, the procedure it to null each zone on the optical surface, using the shadow movement as a guide to that zone’s null. The position of the tester at each null, towards or away from the mirror, measured in thousandths of an inch, is used to decide where the the optical surface needs more work.

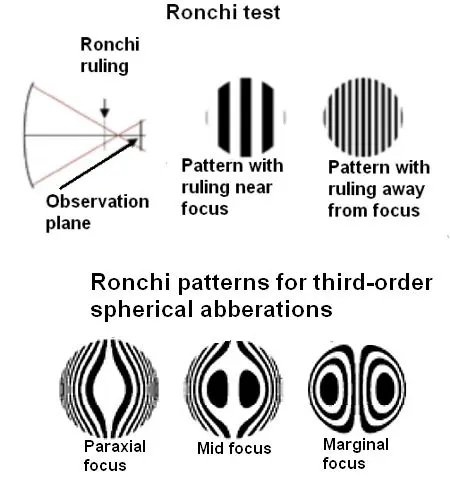
A variant of the Foucault test is the Ronchi test, in which a coarse diffraction grating is used instead of the knife edge. For a perfect lens, the pattern observed is straight lines, with fewer lines closer to focus. Abberations in the optical surface produce distortions in the pattern that have precise relationships to qualities of the lens under test. The resulting Ronchi test patterns are matched to computer-generated patterns to figure out what they say about the optical surface being investigated.

An additional variant is the Caustic test, which is capable of measuring larger mirrors, achieving a λ/20 wave peak-to-valley accuracy. In optics, a caustic is the envelope of light rays reflected or refracted by a curved surface or object, or the projection of that envelope of rays on another surface. The caustic is a curve or surface to which each of the light rays is tangent, defining a boundary of an envelope of rays as a curve of concentrated light. The classic example of a caustic is when light shines on a drinking glass. The glass casts a shadow, but also produces a curved region of bright light. In ideal circumstances (including perfectly parallel rays, as if from a point source at infinity), a nephroid-shaped patch of light can be produced.

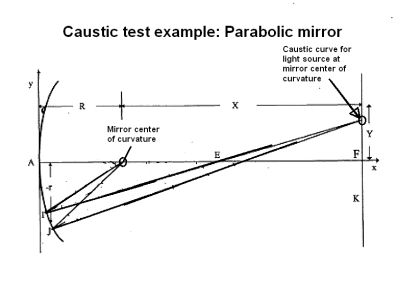The underlying principle behind the caustic test is that the center of curvature for an off-axis segment of a paraboloidal optic surface does not lie on the optic axis. The locus of the centers of curvature, of different off-axis elements of a parabola, lie along a caustic curve. Testing an optical surface thus implies testing it along its caustic curve.

The typical caustic test has an illuminated slit sitting at the paraxial center of curvature for the mirror. The entire mirror is masked except at the points of reflection for the caustic curve. Two images of the slit form at points having a specific relationship to the caustic reflection points and the mirror radius of curvature. If the location of the points is off, the deviation is a precise function of the curvature radius, allowing the computation of the amount of the height deviation at the mirror surface from the exact parabolic shape.