Magnetic flux density and magnetic monopoles

Flux in a magnetic circuit is analogous to current in an electrical circuit. This presupposes the fact that in magnetism, there is a circuit. The parallel to an electrical circuit is not absolute. In an electrical circuit there are two conductors, often called a hot conductor and a return conductor, which is frequently grounded. In a magnetic circuit it is a one-way street, between north pole and south pole.

Even a permanent magnet involves a circuit. If it is a horseshoe magnet with an iron keeper, it is a low-reluctance circuit, or an open circuit. If it is a horseshoe magnet without an iron keeper, it is a high-reluctance circuit. Magnetic reluctance is analogous to resistance in an electrical circuit. The difference is that rather than dissipating energy as heat in the manner of a resistive electrical load, it stores energy in the magnetic field.

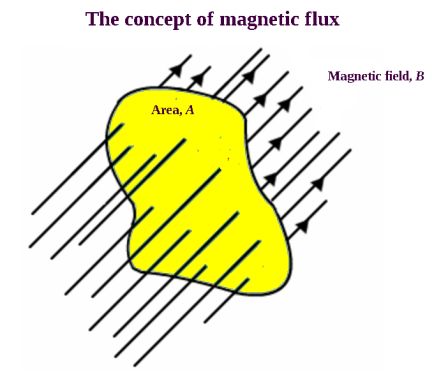
Magnetic flux density is the amount of magnetic flux in an area that is perpendicular to the direction of the magnetic flux. The SI unit of magnetic flux is the weber. The CGS unit is the maxwell. In the SI system, flux density is measured in teslas. One tesla is equal to one weber per square meter. Carrying a charge of one coulomb, a particle that passes perpendicularly through a magnetic field of one tesla at a speed of one meter per second experiences a force equal to one newton.

Magnets have north and south poles. Recently, researchers at the London Centre for Nanotechnology claim to have found magnets that consist of a single pole (monopole) though they say monopoles only exist in a special kind of material called spin ice.

If a bar magnet is cut in half, each half will have a north and a south pole. If the halves are again cut, each resulting quarter will have a north and south pole. If these pieces are ground making fine particles, each grain will be a small permanent magnet with a north and south pole. If the grains are sprinkled over a sheet of paper that has been laid over a large bar magnet, they will align themselves to illustrate magnetic lines of force. The same thing will happen if unmagnetized iron filings are used because in proximity to the bar magnet they become temporarily magnetized.

It will be observed that the lines of magnetic force are closer together above the north and south poles of the bar magnet, and farther apart above its middle region. This is because where the magnetic field is stronger, at the poles, the magnetic flux density is greater.

As an aside, the concept of the magnetic monopole has been controversial. Carl Friedrich Gauss’s Law for Magnetism seemed to leave no room for magnetic monopoles because it asserts that the magnetic field denoted by B has zero divergence. Isolated magnetic charges (in the manner of electric charges as attributed to electrons and protons) do not exist. The conveyors of magnetism are dipolar. For every north or south pole, there is an associated south or north pole.

Maxwell adapted Gauss’s Law for Magnetism, and it became the basis for his second equation. It states that Δ X B = 0. Magnetic field lines neither begin nor end, but take the form of closed loops that extend to infinity and return to the source. The magnetic field is a solenoidal vector field.

That sounds quite definitive, but historically it was not the end of the story. In 1931, Paul Dirac stated that magnetic charges, equivalent to magnetic monopoles, are required by quantum mechanics. If electrical charges are quantized, the notion of a magnetic monopole is absolutely compatible with Maxwell’s Second Equation.

This re-opened the door for the possible existence of magnetic monopoles.