Temporal and spatial aliasing in signal processing

The concept of aliasing is relevant to the oscilloscope user and unless it is confronted and steps taken to mitigate it, problems can arise in signal interpretation. Aliasing is almost always harmful unless clever ways can be devised to make use of it.

When a signal is sampled, aliasing can appear in the end product, and it can be either temporal or spatial. Temporal aliasing is experienced as one watches a high-speed chase in an old-time western movie, where rapidly spinning wagon wheels appear to be turning slowly, sometimes in the opposite direction. You see spatial aliasing when you look through two window screens that are a few inches apart. The scene as viewed through them appears to be comprised of light and dark wave patterns that result from very slight variations in the alignment of the two screens. The same thing is seen in the image of a brick wall when the repetitive vertical and horizontal lines interact with the pixel geometry in a digital camera.

These phenomena seen in everyday life are also realities in the electronics lab when signals are sampled at an insufficient rate with respect to the signal frequency. When this happens, an oscilloscope is likely to render an inaccurate display of the signal, and in that sense aliasing is an apt word to describe what is going on.

An effective remedy for aliasing is to modify the analog signal prior to sampling by deploying low-pass anti-aliasing filters. If you experience a severe instance of aliasing in an oscilloscope display, try placing a low capacitance across the analog input. This circuit simply reduces the bandwidth of the signal of interest so it complies with the Nyquist Theorem, which underlies the whole discussion of aliasing. To see how, we’ll take a closer look at the way in which aliasing arises in the first place.

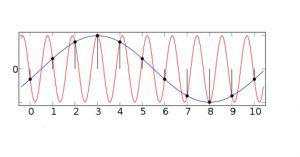
As can be seen in the accompanying diagram, when there is an insufficient number of samples, waveforms may compete to appear on the oscilloscope screen, and various types of distortion can result. A solution to this difficulty, other than bandwidth limiting or signal averaging, is to boost the number of samples taken as part of the digitalization process. So how many samples are necessary to assure that a signal, when digitized, will be free of aliasing?

The answer comes from Harry Nyquist (1889-1976). He formulated what became known as the Nyquist Rate, which quantifies the minimum number of samples that are required to completely and accurately digitize an analog signal, ensuring that it is free of aliasing.

It turns out that to unambiguously digitize a signal, the minimum number of samples taken for each cycle must be two. Conversely, if a continuous function is sampled at the same rate as its frequency, there is an unlimited number of functions that will conform to these samples.

Nyquist’s original work, which appeared in a 1928 paper, promulgated the Nyquist rate in a different context, having to do with data transmission. It specified the maximum number of code pulses that could be conveyed over a telegraph channel of a given bandwidth. Currently, the Nyquist rate is considered applicable primarily in oscilloscope analog to digital conversion.

Pre-aliasing arises in the sampling stage and post-aliasing in the reconstruction stage of an oscilloscope. Either of the operations can cause distortions or artifacts that obscure the actual signal. An anti-aliasing filter reduces these harmful effects by eliminating the portions of the signal that are above the Nyquist frequency.

If you are reading this, you are probably sitting at a computer. For a quick demonstration of the evil effect of aliasing, open a jpeg image and start zooming in. Beyond a certain point, it becomes pixelated and distorted beyond recognition, due to signal aliasing.

In an oscilloscope, sampling takes place in an analog-to-digital converter (ADC). There is one of these for each channel. The process can be easily demonstrated by considering a video camera. The action in real life corresponds to the electrical signal that is fed into an analog channel input in an oscilloscope. The video camera, corresponding to the ADC, takes a series of still shots at a steady, predetermined rate (frames per second). It is essential — if the action is not to be slowed down or speeded up — that the sampling rate remains the same during theater viewing. The periodic nature of the sampling process gives rise to extreme instances of aliasing when the original signal is also periodic, as in an image of a picket fence with uniformly spaced vertical lines.

The Fourier Transform characterizes signals by their frequency content. An aliasing problem during a Fourier transform measurement can render the signal unintelligible because some of the high-frequency information about the signal will be lost. On the contrary, if the bandwidth of the original signal is limited, or if it can be intentionally reduced by the oscilloscope user, the sampling rate rises and the function of interest, now not subject to aliasing, can be rendered correctly.

DAC (digital/analog conversion) can be a source of severe distortion. Indeed, DAC is more difficult to understand than ADC. There are three major parameters: resolution, accuracy (which is not the same) and maximum number of samples that will be required for any conversion. DACs are generally constructed as integrated circuits, in which form they are more user-friendly and less prone to error. However, discrete-component DACs are common in oscilloscopes and other test equipment where high-end sampling is an essential requirement.

A DAC conversion process uses a reconstruction filter to insert continuously varying streams of data between discrete digitized points, so as to paint a realistic analog picture. The aspiration is a smoothly varying signal that is compatible with screen technology and also with human perception.

Because the DAC reintroduces into its output a series of rectangular pulses, there are certain to be harmonics in the output higher than the Nyquist frequency. Where they would negatively impact the finished analog product, a low-pass filter must be placed in adjacent circuitry.

Aliasing is one of a not excessive number of disadvantages of digital compared to analog transmission. Digital communication may be more difficult to understand, but it has distinct advantages as an intermediate step in analog selectivity and processing. While digital must eventually be converted back to the analog domain, as we have seen this transformation can be accomplished within an integrated circuit.