Most electronics engineers and technicians have a good understanding of total harmonic distortion (THD). But there are a few elusive details that come into play during THD measurements.
THD is the ratio of the sum of the powers of all harmonic components to the power of the fundamental frequency. Properly speaking, the fundamental frequency is the first harmonic, but THD discussions frequently don’t acknowledge this fact. THD considers distortion contributed by second-order and higher harmonics but not by the random frequency, broad-spectrum distortion that is known as noise. THD + noise is a separate though important metric.
The familiar sine wave is comprised of a single frequency, while non-sinusoidal waveforms are made up of two or more sine waves that can be added together on a point-by-point basis moving along the time-domain X-axis. Breaking down a complex non-sinusoidal waveform’s sine wave components is a mathematically difficult process but became practical with the advent of the Fast Fourier Transform in the 1960s. Today, one simply imports the nonsinusoidal signal into a spectrum analyzer or, using Math Mode in an oscilloscope, presses FFT. Then, displayed on the screen in real time, is the signal at the channel input in the frequency domain.
Amplitude, in units of power (dB) rather than volts, displays on the Y-axis and frequency, rather than time, displays along the Y-axis. These are the harmonics that, added together and divided by the fundamental, make up THD.
A high THD level in power systems is harmful for the system as well as for connected equipment. Lower THD equates to lower peak currents, higher efficiency and higher power factor.
Power factor is generally thought of as determined by the phase relationship between voltage and current, in accordance with: Power Factor PF = cos θv – cos θi, where θv is the phase angle of the voltage and θi is the phase angle of the current.
While this equation, known as the displacement factor, is valid when voltage and current are sinusoidal, it does not account for THD in non-sinusoidal circuits, which are prevalent today thanks to the rise of nonlinear loads with abundant harmonics.
Loads that include power conversion equipment — such as ac-dc, dc-ac and dc-dc, or nonlinear loads such as fluorescent ballasts — create a heavy nonlinear environment in which harmonics and THD abound. Switching power supplies, now common in office and home, contribute to this mix. This loading modifies the higher-quality sinusoidal power at the utility generator terminals. (Generators do contribute some fifth-order harmonics because of magnetic flux that takes place at the stator slots in addition to non-sinusoidal flux across the air gap.)
VFDs, welders and arc furnaces also generate prodigious amounts of THD.
Because harmonic currents are at higher frequencies that the power system fundamental, they see greater impedances. The cause of this strange phenomenon is that greater amounts of higher-frequency current flow near the surface of a conductor. With less usable cross-sectional area, the effective resistance of the conductor rises, resulting in more heat. This is seen in three-phase neutral conductors and transformer windings.
When an ac motor is powered by a VFD, it gets a powerful direct dose of harmonics. This is a consequence of the high-speed switching in the VFD inverter section. Most of the ambient harmonics caused by other nonlinear loads in the same building or neighborhood are not much of a problem because they generally get suppressed when the power goes through the dc bus midway through the VFD. These outside harmonics do, however, assault the many autonomous motors that are found in the workplace.
For one thing, harmonics create flux distribution in motor air gaps, causing poor start-ups and abnormally high slip in induction motors. A serious problem in motors and generators is pulsating torque, causing losses and mechanical oscillations with harmful heat.
Here’s the greatest problem in motors when there is high THD riding on the good power at the input:
Because of the alternating magnetic field, there is a normal temperature rise in the iron core due to eddy current and hysteresis loss. That is a given, and the iron core is by design sufficiently massive to dissipate this heat. But as it happens, the amount of eddy current loss varies with the square of the frequency. When high-frequency harmonics come along, the heat rises dramatically and, as it dissipates, a significant portion migrates into the windings, adding to the excess heat generated there by the unwanted harmonics and further stressing the winding insulation. Hysteresis varies directly with the frequency, not with its square, but still, it adds to the total.
Another factor, even more harmful, is a loss within the windings. This source of heat varies with the square of the current (I2R) and the harmonics have a significant negative impact. Additionally, these high-frequency components exhibit harmful skin effect, reducing effective conductor size.
If a generator is to supply nonlinear loads, it should be derated because it has higher reactance and impedance than a similar size motor. Combined with high-frequency magnetic flux resulting from the presence of powerful harmonics, they boost the stator temperature. Rotor heating also results from these high-frequency currents.
Additionally, harmonics set the stage for often catastrophic transformer failure. Generally trouble-free, transformers without warning may explode as big nonlinear loads abruptly switch on. The problem is compounded in older transformers containing toxic PCB-laden cooling oil.
Copper and iron losses combine to create a hazardous situation. Eddy current rises when harmonics enter a transformer from line or load. Because eddy current is proportional to the square of the applied current and the square of its frequency, a transformer catastrophe can happen suddenly and without warning.
Harmonic current in transformers is a source of electromagnetic interference that can degrade nearby communication circuits. Shielding, increased spatial separation and suppression of the harmonics are used to mitigate these effects.
To summarize, Fourier analysis (as opposed to Fourier synthesis), of a periodic signal reveals the harmonic frequencies that are components and integer multiples of the signal. This is where THD appears.
The reason that a voltage and its associated current are purely sinusoidal is that they consist of a single frequency. Multiple higher frequency components contribute to the observed THD. A square wave has a great amount of this distortion while a sine wave that is in the real, non-ideal world has a small amount of it. In most cases, that component is not visible in the time domain, but it can usually be observed just above the noise floor in the frequency domain.
THD is a constant concern in power systems. Low power factor, higher peak currents and low efficiency accompany high THD. In audio reproduction, a low THD equates to better fidelity. In communications systems, high THD means a potential for interference with nearby equipment and greater power consumption at the transmitter.
A THD analyzer can be used to measure the distortion of a waveform in comparison to a distortion-free sine wave. The instrument breaks the wave under investigation into its harmonics and compares each harmonic to the fundamental. An alternate procedure is to remove the fundamental by means of a notch filter, then measuring the remaining signal which will be the THD plus noise.
In audio equipment development, a low-distortion arbitrary function generator is used to insert an input into the unit being evaluated. Distortion at constituent frequencies is then measured for comparison of prototypes. In such procedures, crossover distortion for any given THD level is more audible and thus tends to outweigh clipping distortion, which produces higher-order harmonics.
Generally, harmonics are beneficial only to the musician, who uses them in a flute or guitar to produce sounds that would otherwise be beyond the capability of the instrument.
The best way to mitigate harmonics is to suppress them at the source. An alternative is to create shielding or filters at the equipment that is affected by the harmonics. Then, measuring the amount of THD, the success of these measures can be evaluated.
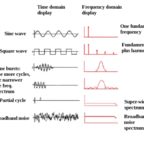

Every wave form can decomposes into square waves as well, something that can be used to generate waves with a digital processor.
Great article and it explains well the heat rise in VFD applications. I have spent many years in my career warning installers of this phenomena and what it can do the motor, the windings and the electrical connections. Often these connections are made with thermoplastic insulation such as PVC or THHN that are not able to withstand the sudden heat rise. When moisture is in the application, the challenge is even greater as PVC wiring for example loses a large portion of its ability to insulate when wet. Thermoset XLPE cables designed for such an application will withstand the electrical and thermal challenges of VFD applications. The switching frequency of IGBT’s has increased quite a bit over last decade but few measures are being taken to deal with the harmonics to save cost. The only standard that currently addresses this is the NFPA 79 article 4.4.2.8 “Circuits supplied from Power Conversion Equipment”. The next 2020 NEC may at least offer some informative language about the phenomena in section 430. Mitigating harmonics is a multi-pronged approach by using filters, chokes, thermoset insulated VFD cables and proper grounding techniques.
“Generators do contribute some fifth-order harmonics because of…” Nope, not even close. Which harmonics are created is determined by the Bullard Harmonic Solution, nothing else. Harmonics are created in proportion to their AREA in the transfer function, minus the EVEN harmonics that are cancelled by symmetry. And all harmonics are phase related to the fundamental at either 0, 90, 180 or 270 degrees relative to the fundamental sine wave (0 or 180 if you look at the fundamental as a cosine wave). Learn about the Bullard Laws of Harmonics (goggle it),