A Smith chart provides insight into RF/microwave designs. Even if you work primarily with low-speed analog and mixed-signal designs, you could benefit from familiarity with the Smith chart as wireless products proliferate and as high-speed-serial data signals exhibit microwave-like effects.

When a signal’s wavelength (λ) approaches the lengths of the conductors carrying it, you can no longer rely on the lumped-element impedance model represented in Figure 1, in which perfect conductors carry currents traveling at infinite speeds.
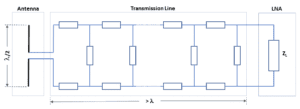
With RF signals, think instead of a transmission line consisting of an infinite series of distributed impedances (Figure 2). The Smith chart simplifies calculations involving complex numbers in the form of x + jy, which come up frequently in RF/microwave designs that involve transmission lines and require impedance matching.
Why do impedance matching?
Two reasons. First, given a source with a fixed impedance (50 Ω in Figure 1), the maximum power transfer theorem states that the maximum amount of power transfers to a load if the load impedance matches the source impedance. Figure 3 plots load power (red curve) vs. various load impedances (horizontal axis), showing that the load absorbs maximum power when it matches the source’s impedance. You are probably familiar with this theorem. The values shown in Figure 1 approximate what you might find working with a receiving antenna, but the theorem applies to DC and low-frequency designs at high voltages as well. (Note that an antenna signal level would generally be expressed in dBm, not µV, but the voltage value helps show how the theorem works.)
Yes, but something doesn’t sound right — if the impedances match, how could efficiencies ever be higher than 50%?
Note that the theorem says nothing about designing source impedance to match a given load impedance — for DC designs, you should minimize source impedance regardless of load impedance. The black trace in Figure 3 plots efficiency, which indeed is 50% at the 50-Ω point, but efficiency continues to climb as the load impedance increases, although overall power falls.

The theorem applies when you have a fixed, unalterable source impedance. If, as in Figure 2, you are using a half-wavelength dipole antenna to receive a signal, the antenna presents a source impedance of (73 + j45) Ω, which you must consider when choosing a transmission line, low-noise amplifier (LNA), or other components.
So, I should match impedances when receiving a signal but minimize source impedance when transmitting?
No! I mentioned there are two reasons for impedance matching at RF frequencies. The second is to minimize reflections that impedance mismatches cause, calculated using the reflection coefficient Γ:
This equation shows that if ZS = 50 Ω and ZL = 150 Ω, half the incident power will reflect back from the load to the source. The reflected power never reaches your antenna and is dissipated as heat, possibly damaging your transmission line and power amplifier.

OK, I’m sold on impedance matching. How does the Smith chart help me?
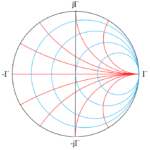
The Smith chart includes a plot of $Gamma; and overlays it with circles and arcs representing impedance to allow you to relate to source, line, and load impedances. In Figure 4, Γ equals 0 at the origin, and its magnitude is 1 along the outer black circle. Each blue circle and red arc represent a locus of points of constant resistance and reactance, respectively.
Part 2 will add some specific numbers to this chart and demonstrate some calculations.
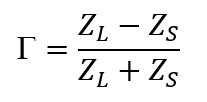



Leave a Reply
You must be logged in to post a comment.