Newton’s Law of Universal Gravitation — as well as a number of other relations in such diverse fields as electric, magnetic, light, sound and radiation propagation — conforms to the inverse square law. This law states that intensity is inversely proportional to the square of the distance from the source.
Newton’s law provides that any two bodies in the universe attract each other with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
Similarly, Charles Coulomb’s law quantifies the electrostatic attraction or repulsion between particles that have an electrostatic charge. It states that the magnitude of the electric force between these charged bodies is directly proportional to the product of the charges and inversely proportional to the square of the distance between them.
Reduction of sound intensity with distance also conforms to the inverse square law, but the observed effect in a large auditorium is more complex due to a variety of reasons. The reduction of sound intensity in a closed room from 20 feet to 200 ft. would be by a factor of 100, or 20 decibels. This great loss, however, is partly counteracted by reverberation.
In human midrange, a 20-dB drop would seem one-fourth as loud. In the low range, there is a greater loss in perceived volume, known as bass loss. In an auditorium, the size and shape of the room — including ceiling height, wall and seat texture, number of occupants, and other factors — combine in complex ways to create the final effect.
These laws and others like them are analogous. Substitute a few words and they are identical. It is easy to see that the effect of the two bodies diminishes with distance, but why the exponent two?
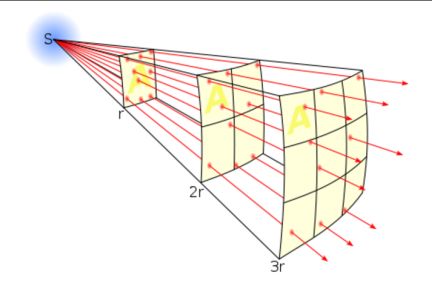
It is a consequence of simple geometry in three-dimensional space. If we assume, as usual, that the two bodies are point sources or spherical objects that emit energy equally in all directions, then this energy will appear in the form of a spherical shell advancing at a uniform rate. The intensity of the energy is inversely proportional to the area of the shell, which grows in size as time elapses and it moves away from the source.
The mathematical relationship between the distance traveled (radius of the sphere) and intensity of the energy (area, not volume, of the surface of the sphere) is expressed by the equation:
A = 4πr2
And that is the reason for the square in these laws.
Radar (Radio Detection and Ranging) is one of the entities that behaves according to the inverse square law. It has its roots in the work of Heinrich Hertz (1857-1894) and other late nineteenth-century researchers who found that radio waves could reflect from solid objects. The implications became more fully realized in the first years of World War II when British electronic engineers developed means to detect hostile aircraft coming their way across the Channel.
Since then, radar systems have become far more elaborate and have expanded into numerous non-military applications. Radar is capable of providing information concerning the bearing and distance of objects from which can be derived their exact location. Additionally, the composition and shape can be ascertained, and Doppler radar can determine an object’s speed moving toward or away from the observer.
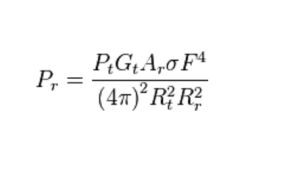
F = pattern propagation factor, Rt = distance from the transmitter to the target, Rr = distance from the target to the receiver. When the transmitter and the receiver sit at the same place, Rt = Rr and the term Rt² Rr² can be replaced by R4, where R is the range. So the received power declines as the fourth power of the range.
This information is obtained by a transmitter-receiver combination, usually in the same location and often using the same antenna on a time-allocation basis. The beam of electromagnetic energy is aimed at the object of interest. Electrically conductive materials including most metals, carbon fiber, seawater, mineral deposits to different degrees and relatively moist air are highly reflective and show up well on radar.
The frequency of the signal transmitted determines the resolution of the received image. Early models used low-frequency signals and consequently only large objects could be imaged. Currently, centimeter-range signals are capable of discerning small targets.
Polarization is an important factor in the design of radar equipment. For various purposes, polarization may be horizontal, vertical, linear or circular. Different polarizations are appropriate for individual reflections. Circular polarization, for example, reduces interference from rain, and this is essential for radar-assisted aircraft navigation in bad weather. Linear polarization in the received signal indicates a metallic object of interest while random polarization results from irregular surfaces such as the air-ground interface.
Though radar signal intensity does obey inverse-square relationships, many other factors bear on the signal. If the medium through which the signal passes is other than a vacuum there will be attenuation, the amount dependent upon the material and the distance traversed. Moreover, while the beam may be aimed parallel to the earth’s surface, over significant distances the earth’s spherical shape is relevant. Another variable is that the refractive index of air varies with altitude and moisture content.
Because reflected signals fade rapidly with distance, eventually dropping below the noise floor, signal-to-noise ratio becomes critical. Noise may be internal, as generated in all electronic components, or it may be external, either intentional as in jamming or environmental as in thermal background radiation.
Recent advances in signal processing have mitigated limiting factors including noise and partial barriers to the transmitted and reflected signals, and additional refinements can be expected.

Both wonderful and well-written. Thank you.