A conic section is formed by the intersection of a plane that cuts though a cone, usually with the circle at the top and the hyperbola at the bottom. Between them lie the ellipse and the parabola.
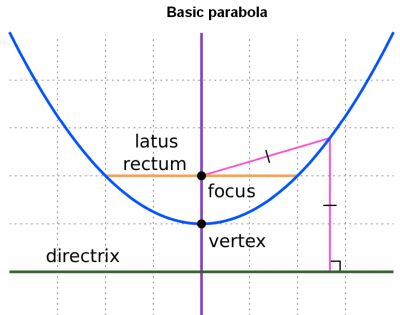The parabola has distinctive properties when rotated in space to make a concave surface. The parabola can be defined, like other conic sections, from multiple perspectives. A parabola is set of all points in a plane which are an equal distance away from a given point and given line. The point is called the focus of the parabola, and the line is called the directrix. The directrix is perpendicular to the axis of symmetry of a parabola and does not touch the parabola. Parabolas are also generated by the intersection of a conical surface and a plane parallel to another plane that is tangential to the conical surface.
Most important for a parabola is the distance between the focus and vertex, which is the focal length. When a parabola is mounted and pointed with the conical surface directed toward a source of light, light that travels parallel to the axis of symmetry will be precisely reflected to the focus. Alternately, light from a point source at the focus is reflected to form a collimated beam. The parabolic surface exhibits the same dual properties with other forms of radiation and with sound. This behavior has been exploited to create numerous useful devices such as, perhaps most notably, parabolic antennas, microphones, and automotive headlight reflectors.
That brings us to the subject of DIY parabolic antennas that aren’t really parabolic. It’s possible to find YouTube videos describing the construction of reflector dishes mainly used to boost the range of WiFi signals. But the construction techniques outlined make it clear that the resulting reflector dishes aren’t parabolic in shape but rather trace out a catenary curve.
A catenary is the curve traced out by an idealized hanging chain or rope hanging under its own weight when supported only at its ends in a uniform gravitational field. The catenary curve can superficially resemble a parabola, but it is not a parabola. Mathematically, the graph of y = x² is a parabola and the graph of y = cosh(x) = (ex + e–x)/2 is a catenary. The point to note when considering a catenary as an antenna shape is that it doesn’t have a focus point like a parabola does. That hasn’t stopped YouTubers from describing how to make antennas shaped by catenary curves.
The usual approach to fabricating a catenary dish antenna starts with hanging a length of chain between two points just in front of piece of plywood. Spray painting the chain then leaves a shadow on the plywood that traces out the catenary curve. Jig sawing along the shadow yields a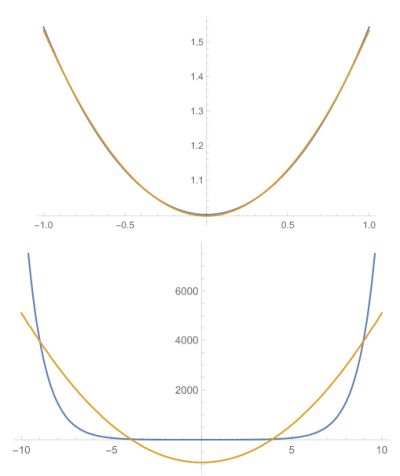 
The primary reason catenary shapes can approximate parabolics is that the two kinds of curves can be approximately the same if the dimensions are just right. The best explanation of this we’ve found comes from John D. Cook Consulting. The key is that vertical distance involved in the catenary solid of revolution must be on the same order as the outer diameter. The catenary becomes extremely un-parabolic as the vertical dimension exceeds the solid of revolution diameter. Cook illustrates this by computing the error of a least-squares fit between a parabola and a catenary over a given interval.
The lesson seems to be that antennas having a catenary solid of revolution can mimic parabolics so long as when you eye-ball their dimensions, you have a hard time telling the two types of curves apart.
Leave a Reply
You must be logged in to post a comment.