Bandwidth is a principal specification when choosing an oscilloscope or related instrument. What it means in this context is a displayed signal’s maximum frequency above which the scope attenuates the amplitude of the signal it sees. Problem is, this isn’t the only definition of bandwidth. The concept has slightly different meanings (and consequences) depending on the context, a fact that can be confusing to those just beginning their technical career. For those in that category, here’s a quick bandwidth-for-dummies-type explanation.
Among its many uses, bandwidth may be taken to refer to the extent of spectral width, a bit rate of data transfer or, in atomic physics, spectral line-width. In linear algebra, bandwidth is the width of non-zero terms around a matrix diagonal. It also means graph bandwidth or coherence bandwidth, which is the deviation over or under a frequency in which a channel is said to be flat.
Power bandwidth refers to the span of frequencies in which an amplifier’s power is greater than a specified fraction of its rated power. Additionally, bandwidth has some trivial meanings such as in business or political jargon–generally it is slang for capacity.
An easy way to visualize bandwidth is to consider the frequency range of a base-band signal amplitude-modulating a carrier as in AM radio. At any instant, the conveyed signal consists of the carrier frequency, the carrier frequency plus the frequency of the audio modulating it, and the carrier signal minus the modulating audio. Bandwidth consists of the spectral distance between the high- and low-frequency extremes.
One ambiguity surrounding bandwidth pertains to the Nyquist Sampling Theorem. Here, bandwidth equates to the baseband frequency spectrum, whereas in the Nyquist Symbol Rate, or Shannon-Hartley channel capacity, we are talking about passband frequency spectrum.
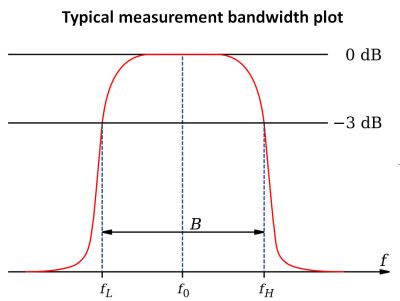
Now consider a single pulse. When viewed in the frequency domain, its frequency content on either side of its fundamental frequency trails off in both directions to infinity or, if bounded, it trails off some finite spectral distance. To realistically quantify bandwidth, an attenuation limit must be set, and this is generally -3 dB relative to the maximum value. At the -3 dB point, the spectral density is 50% of its maximum value. The spectral amplitude, V/√Hz, is 70.7% of its maximum.
The first signal display instruments had by modern standards extremely low bandwidth, often because their recording implementation had mass and inertia as for pen-and-ink assemblies that would draw the waveform on a rotating paper cylinder. Things changed with the invention of the oscilloscope. Allen Dumont’s 1943 Model 224-A, with a three-inch cathode ray tube, provided a 2-MHz bandwidth. It was followed in 1945 by a 5-MHz scope. By 1956, Tektronix was selling 24-MHz instruments, and in 1960 Hewlett-Packard’s 185A attained 500-MHz bandwidth, followed by the first 1-GHz model. By 2009, Tektronix was offering a 20-GHz mixed-signal model and in 2010 a LeCroy scope hit 45 GHz. In 2018 Keysight broke the record at 110 GHz.
All these ultra-high bandwidth oscilloscopes are extremely expensive. The good news is that costs have dropped for lower-bandwidth instruments loaded with features and capabilities. It’s now possible to find 100-MHz scopes on Amazon for under $300.
For measuring digital signals, the oscilloscope should have a bandwidth five times higher than that of the fastest clock rate in the equipment under investigation. In analog applications, this factor can be reduced to three.
Though it may seem counter-intuitive, you should avoid using an oscilloscope having too much bandwidth. Because noise occurs at all frequencies, an instrument with higher bandwidth than necessary for the measurement at hand will add excessive noise to the signal as displayed and provide inaccurate measurements. Modern scopes invariably include an option for reducing bandwidth. It must be emphasized that this does not reduce the bandwidth of the instrument. It merely temporarily adjusts the bandwidth of the signal being accessed.
Why would anyone do such a thing after paying all that money to acquire a high-bandwidth instrument? The answer is that it is a successful strategy for reducing noise that is obscuring an otherwise clear signal. Because noise is a broad-spectrum phenomenon that extends throughout the full bandwidth of the instrument, reducing bandwidth removes a substantial amount of noise from the acquisition. Of course, this procedure succeeds only when part of the signal of interest is not lost in the process.
The procedure is usually quite similar for all scope brands: With the noisy signal displayed, press the Channel On button to bring up the horizontal menu. Then press the (usually) soft key associated with Bandwidth. The Vertical Bandwidth menu lets the user select the amount of bandwidth reduction–typically in a 1-GHz oscilloscope, Full (the default), 250 MHz or 20 MHz.
Among all its technical meanings, in this Internet Age, bandwidth has come to denote the volume of information per unit of time that can be conveyed across an Internet connection. In this context, bandwidth is given as bits per second, meaning the maximum data transfer rate per second. In most consumer local area networks, gaming consoles and video streaming services account for the greatest bandwidth use. Available bandwidth of an individual Internet connection can be determined by online Internet test sites.
Regardless of its location in the overall frequency spectrum, a signal having a specific bandwidth is capable of carrying a finite amount of information without respect to its spectral location. In RF communications, bandwidth is the frequency range required by a modulated carrier wave to convey the intended signal reasonably free of excessive distortion or attenuation. Signal bandwidth measured in Hertz is the frequency range in which spectral density is held close to zero, generally expressed in decibels.
System bandwidth refers to the range of frequencies in which the system can efficiently process signals. Fractional bandwidth is the ratio obtained by dividing the bandwidth of a device by its center frequency, usually expressed as a percentage.
The Rayleigh bandwidth of a radar pulse is the inverse of its duration. Thus, if the Rayleigh bandwidth is 1 MHz, the duration of the radar pulse is one microsecond. The essential bandwidth is the portion of a signal spectrum which contains most of the signal energy.
The Shannon-Hartley bandwidth is the 3-dB range in which the gain is a finite quantity based on the Nyquist sampling rate and maximum bit rate specified in the Hartley formula. In control theory, bandwidth is a specific frequency in which the closed-loop system gain is held at or below 3 dB referenced from peak amplitude.
Bandwidth is applicable in light as well as electrical transmission. For example, it is the measure of the frequency range conveyed through an optical waveguide, or the gain of an optical amplifier. It is also the frequency range of an optical modulator or power meter. A related metric is the bit rate in an optical communication system.
An important metric is bandwidth efficiency. Also known as spectral efficiency, it is the rate at which information can be conveyed over a specific bandwidth. It is dependent upon the physical layer characteristics and channel access protocol.
Link spectral efficiency is measured by bit/sec/Hz. It is equivalent to the net bitrate divided by the bandwidth. An alternate interpretation is that it is bit/symbol, or net bitrate/symbol rate, which is the line code pulse rate. Modulation efficiency is bitrate/bandwidth.



Leave a Reply
You must be logged in to post a comment.