It was once widely taught that entropy is a measure of disorder. Educators increasingly feel that the concept of entropy as the disorder can be confusing. So increasingly the “disorder” explanation is giving way to the idea that entropy describes energy spreading out or dispersing. The usual ways energy spreads out is when the system increases in volume or when the system is heated. The principle can be easily demonstrated in the lab or even as a simple table-top demonstration at home.

Into a vessel of clear water, introduce a small amount of black ink. The ink will mix with the water, quickly dissipating and becoming invisible as its concentration decreases. The ink mixes with the water, at first due to the collision between the two substances, and finally due to random molecular motion. You can look at this as the ink dispersing because it has experienced an increase in volume. It is conceivable that the process would reverse so that the ink molecules would reconstitute and form once again into a black blob, but probability working in conjunction with the arrow of time predicts otherwise.

The phenomenon known as entropy has been formalized as the second of these three laws of thermodynamics:
• The first law of thermodynamics asserts a universal conservation of energy, stated in the context of thermodynamic systems. Energy can change from one form to another, but it can be neither created nor destroyed. The pressure of a gas, for example, can decrease, but simultaneously its temperature will decrease while its caloric energy content remains constant. This makes possible the seeming paradox of refrigeration.
• The second law of thermodynamics is the one that disallows decrease of entropy with respect to time.
• The third law of thermodynamics emerged in the early 20th century. There are several versions, the most basic statement being that the entropy of all perfect crystalline solids is zero at absolute zero temperature.

Thus entropy can be viewed as a measure of energy dispersal as a function of temperature. In chemistry, the kind of energy that entropy measures are both the motional energy of molecules moving around and vibrating and phase-change energy (enthalpy of fusion or vaporization). Put another way, entropy measures how much energy is spread out in a process over time or how spread-out the initial energy of a system becomes (at constant temperature). It is mathematically simple to compute exactly how much energy is dispersed in a phase change or temperature change.

Most often computations of entropy are actually computations of an entropy change, the measurement of a change in the amount of energy dispersal in a system (or surroundings) before and after a process. Only for perfect crystals at absolute zero degrees can entropy be represented by a single measurement, 0 joules/K — entropy itself is traditionally described with the units of J/K.

The standard state entropy of any substance at 298°K can be read from tables. The usual units found in entropy tables is J/mol K. Standard entropies of formation are given in molar quantities this way because they assume you are creating one mole of the substance.

One well-known statement of entropy is Boltzmann’s equation, a relationship relating the entropy S of an ideal gas to the quantity W, the number of real microstates corresponding to the gas’ macrostate: S = k_B ln W where k_B is the Boltzmann constant (also written as simply k) and equal to 1.38065 × 10⁻²³ J/K, and W is the number of microstates. W can be counted using the equation: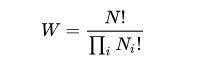

for an ideal gas of N identical particles, of which N_i are in the i-th microscopic condition (range) of position and momentum, and i ranges over all possible molecular conditions. Basically, the Boltzmann formula shows the relationship between entropy and the number of ways the atoms or molecules of a thermodynamic system can be arranged.

Obviously, all this gets high theoretical — one can’t really count all possible molecular conditions. Consequently, the entropy change between two thermodynamic equilibrium states of a system is often measured experimentally. The task involves devising a reversible path between the initial and final states for which the heat flow can be measured somehow. In the real world, there is no perfectly reversible path, so experimenters go for something that is as reversible as possible. It can also be difficult to measure the amount of heat flow, so it is sometimes done indirectly. An example might be measuring the isothermal quasistatic expansion of a gas stoked by a heat bath. The measured amount of work could be how hard the gas pushes on a piston, determined perhaps by incrementally removing small weights on the piston. This would be equal to the amount of heat added.

The three laws of thermodynamics were formulated at different times by different theoreticians, but are now considered a single framework for understanding entropy, particularly as it relates to the one-way nature of time. A video sequence can be run in reverse, giving us an idea of how things look where the laws of thermodynamics do not apply. But as far as we know, time cannot be reversed, so these laws are absolute.

The second law of thermodynamics has drawn great interest over the years because it prohibits order in a closed system from increasing with respect to time. An essential concept is that this law is applicable only to a closed system. An air-conditioner, cooling a single room, creates a lower entropy situation because the air molecules exhibit less random motion. However, to function properly, an air-conditioner always vents hot air to the outside. Accordingly, the region of decreasing entropy is not a closed system and the law does not apply. Due to mechanical friction and electrical resistance, surplus heat is actually created, so entropy overall rises.

Naturally, following its publication, many theorists and experimenters sought to contradict the second law of thermodynamics, either by means of a convincing counter-example or on theoretical grounds. They reasoned as follows:

As time progresses, it is asserted that closed systems move toward thermodynamic equilibrium, exhibiting greater entropy. An example is the temperature of a gas in a sealed box, which will in time become uniform throughout the container. If faster moving molecules under some conditions could be observed to migrate to one side of the container, leaving behind the less energetic, slower particles, the second law of thermodynamics would be overthrown. This could take place with the aid of some sort of machine, chemical process or other mechanism provided higher-energy particles did not leave the sealed box as in a conventional room air-conditioner.

Entropy reduction with respect to time in a closed system might be difficult to achieve, even under optimum laboratory conditions, but a unique thought experiment soon suggested itself, and it posed a substantial threat to the second law of thermodynamics. This thought experiment was the creation of James Clerk Maxwell (1831-1879). He proposed, first in a letter to a colleague and then in his treatise on thermodynamics, Theory of Heat (1872), a thought experiment that challenges the second law of thermodynamics.

He envisioned a demon who opens and shuts a small door in a partition that divides two sections of a sealed vessel containing a gas. As a randomly moving gas molecule approaches the door, the demon selectively opens or closes it, admitting fast/hot particles and excluding slow/cold ones. This is a two-way process – otherwise one side would become more pressurized than the other. Eventually, there is a preponderance of low-energy molecules in one section and high-energy molecules in the other section.

To overthrow the second law of thermodynamics, we have to stipulate that the vessel is sealed and thus isolated from the outside world, and furthermore that the demon is sealed in the container, on one side or the other of the partition. Maxwell’s thought experiment concludes that because molecules with greater kinetic energy are hotter, the container on one side of the partition exhibits higher temperature than the other side and entropy decreases with respect to time in this closed system, contradicting the second law of thermodynamics.

Soon theorists proposed arguments attempting to invalidate Maxwell’s reasoning. The intent was to reaffirm the second law of thermodynamics, first by demonstrating that the energy required for the demon’s actions in separating fast and slow molecules would, in fact, create greater entropy. One would think that the act of opening and shutting the door would tip back the balance, but actually, most contra-demon arguments have been somewhat more subtle, focusing instead on the act of acquiring and storing the information relating to energy states of the individual gas molecules.

Acquiring information by the demon implies an expenditure of energy. Due to the interaction between the gas and the demon, it is the total entropy that is relevant. Entropy increase of the demon is sure to be greater than entropy lowering of the gas.

The discourse between pro- and anti-demon theorists reached a new level in the 1960s when it was proposed that an act of measurement may not necessarily increase entropy in a closed system provided that the measuring process could be thermodynamically reversible. Notwithstanding that the reversible measurement could be seen to violate the second law of thermodynamics, a way out of this impasse consists of deleting the demon’s information rather than storing it beyond a critical point. The thinking is that once the molecule is moved, the information concerning its pre-move status is no longer required.

It is hard to believe, but in 2012 University of Stuttgart physicist Eric Lutz and others devised a real-world experiment that measured the minimum energy dissipated by deleting information. They confirmed that to approach this limit, the system must come close to zero processing speed.

In defense of Maxwell’s initial position, subsequent researchers have argued that anti-demon opponents prejudge the matter by assuming that the demon cannot in principle violate the second law of thermodynamics. They assert that it is questionable to assume the erasing of information requires significant energy consumption. In any event, it is circular reasoning to defend the second law of thermodynamics solely on that basis.

This argument addresses the consistency between the second law of thermodynamics and the demon strategem for challenging it, but a more recent interpretation reopens the question from a new perspective. It is based on non-equilibrium thermodynamics for small fluctuating systems in which measurement is seen as a process where mutual information between the system and demon increases. Through a feedback loop, that correlation decreases, and once again the second law of thermodynamics is challenged.

In the emerging field of nanotechnology, it is now possible to build a Maxwell’s demon container in which individual molecules are manipulated. It has been theorized that if mirror matter exists, it may be feasible to vent entropy-encumbered particles into the mirror world and actually construct a heat engine that does not require fuel.