What is intermodulation, and is it good or bad? Part 2

A mixer can upconvert and downconvert a modulated signal with no loss of baseband information.

Part 1 of this series described intermodulation resulting from the combining of two or more sinusoidal signals through a nonlinear device such as the mixer in Figure 1. The mixer’s output is the product of its two inputs, and its output’s frequency content is f₁+f₂ and f₁–f₂. The frequencies f₁ and f₂ do not appear in the output (unless it is f₁=f₂, in which case the output contains f₁=f₂ plus a DC component).

Figure 1. A mixer’s output includes the sum and difference of its input waveforms’ frequencies.

That brings up the question: if f₁ in Figure 1 is a carrier and f₂ is a message signal that we want to use to modulate the carrier, does the carrier disappear during the modulation process?
It depends on the modulation scheme. Here is the equation for a version of amplitude modulation (AM) called double-sideband suppressed-carrier (DSBSC) modulation:

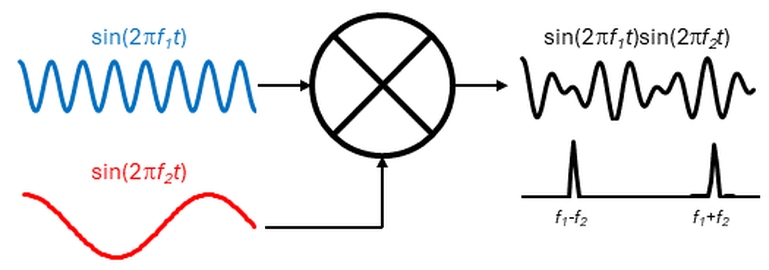
Here, f_M is the message signal we want to use to modulate the carrier f_C. Figure 2a shows the modulated waveform (blue) for f_C equals 1,200 kHz and f_M equals 50 kHz (red, with the gray curve representing negative f_M). Figure 2b shows the fast Fourier transform (FFT) of the modulated signal. Here, the original 1,200-kHz carrier doesn’t appear—only the sidebands at 1,150 kHz and 1,250 kHz—that is, ±50 kHz from 1,200 kHz.

Figure 2. The DSBSC signal (a) includes sidebands, but the original 1,200-kHz carrier signal doesn’t appear.

What about conventional AM without the suppressed carrier?
Here’s the relevant equation:

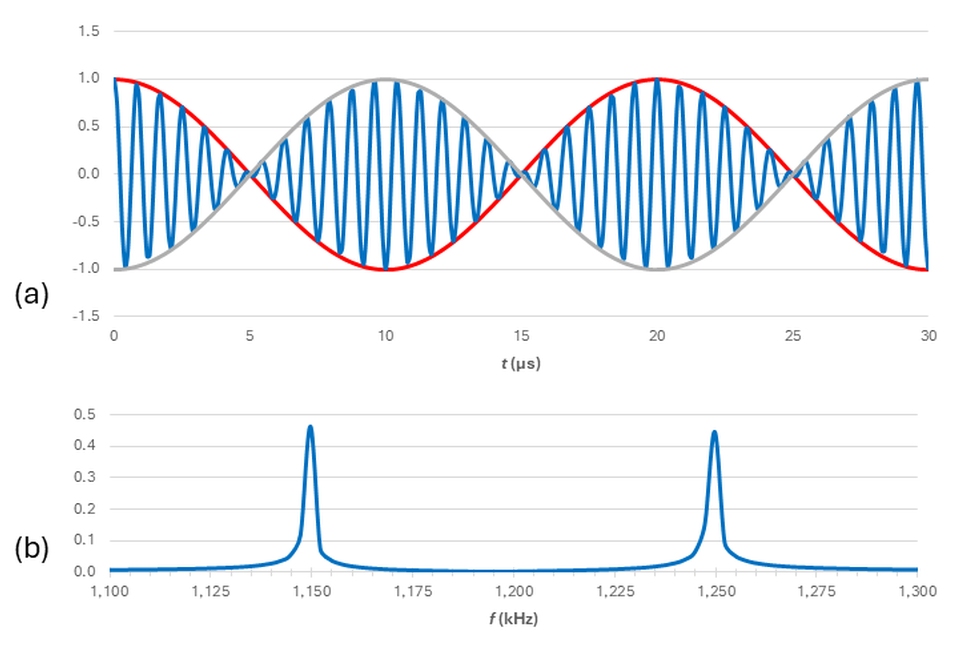
Figure 3a shows the time-domain representation of f_AM(t) for the same frequencies used in Figure 2. Note that in the conventional AM equation, the term to the immediate right of the equals sign isn’t multiplied by any other variable. Also note that in Figure 3a, the absolute value of the carrier-envelope (gray) is always greater than zero. Figure 3b shows the FFT. Here, the carrier does appear explicitly, with the sidebands offset by ±50 kHz.

Figure 3. The time-domain representation of a conventional AM signal (a) yields an FFT (b) that includes the original carrier.

What’s another good use for intermodulation?
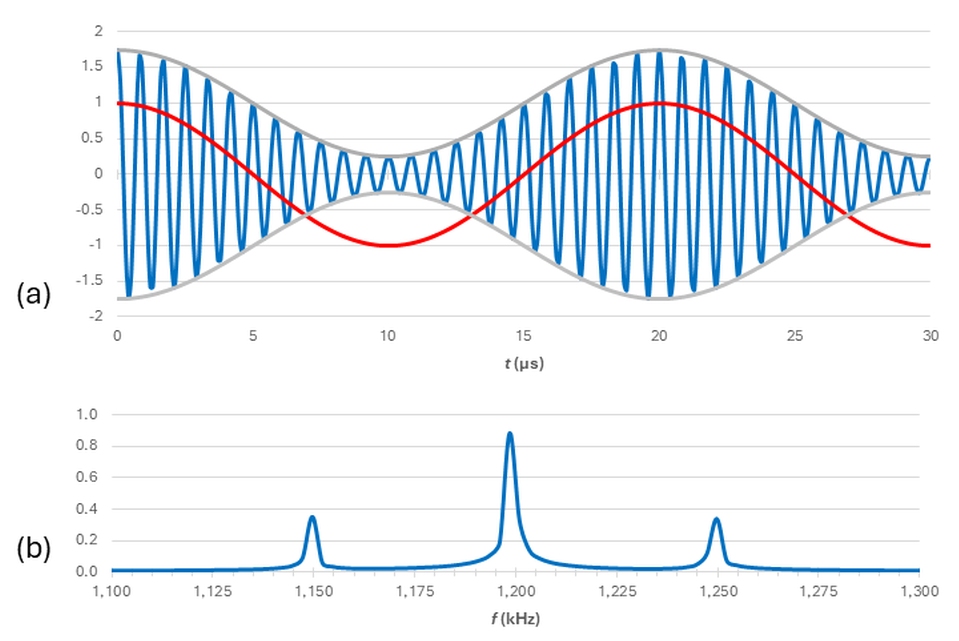
Say we don’t want to use the 1,200-kHz carrier in Figure 3. Intermodulation lets us translate the carrier and its accompanying sidebands to other frequencies. For example, Figure 4a shows the modulated carrier from Figure 3a (blue) and a 900-kHz cosine wave (red). Figure 4b shows the product of those two waveforms (obtained by combining them in a mixer).

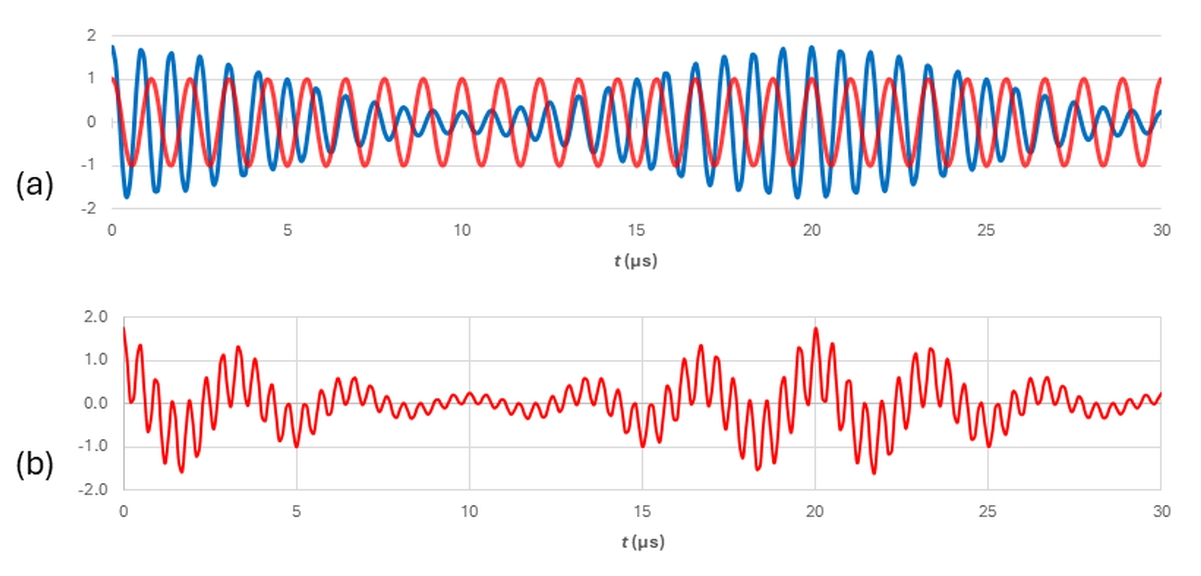
Figure 4. Combining the Figure 3 modulated blue waveform and 900-kHz red waveform (a) in a mixer results in the waveform representing the product (b).

Figure 5 shows the FFT of the Figure 4b waveform. Note that the 1,200-kHz carrier and its sidebands have disappeared; I’m showing them as a dotted blue trace for reference. The 1,200-kHz carrier has been downconverted by 900 kHz to 300 kHz and upconverted by 900 kHz to 2,100 kHz, with the sidebands maintaining their ±50-kHz offset from each carrier, as emphasized in the insets. The key point here is that the frequency-translation process does not interfere with our ability to retrieve our original baseband message.

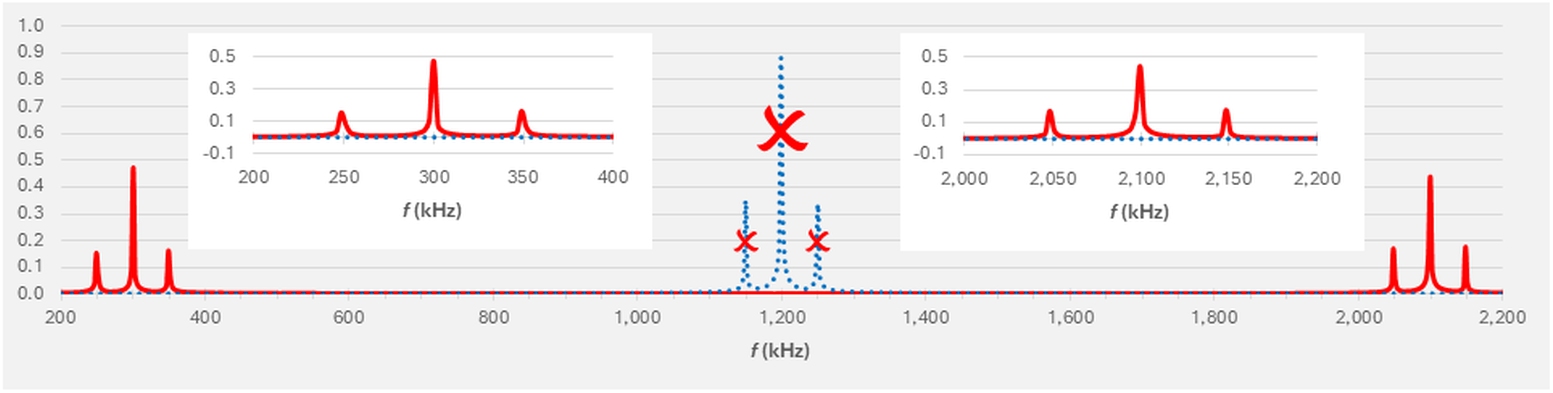
Figure 5. The FFT of the Figure 4b waveform shows that the Figure 3b carrier and its sidebands have been downconverted and upconverted by 900 kHz.

Don’t 50-kHz sidebands seem unusual for AM?
Yes. Typical AM would be better represented by 5-kHz sidebands on carriers from about 560 to 1,700 kHz, and the sidebands wouldn’t be peaks but rather approximations of continuous functions that taper off near the sideband limits. I chose the parameters here to enable both the downconverted and upconverted carriers in Figure 5 to appear on the same chart with sufficient resolution so that the sidebands would still be clearly visible. To produce the FFTs in this post, I used Microsoft Excel, as described in a recent series. In part 3, we’ll take a quick look at the reasons for choosing the parameters and settings I used. That will conclude our look at the good uses of intermodulation, and we’ll turn our focus on the bad: intermodulation distortion (IMD).